Boeing has been in the news a lot recently for all kinds of apparent malfunctions and issues. Last night, I noticed Joe Weisenthal ask whether this represented a real problem or confirmation bias (as can happen when our collective attention is newly trained on an issue). I wondered the same thing, and before this analysis I was unsure whether Boeing or Airbus are safer. So I decided to collect some data and check for myself.

Before I begin, it’s important to note that traveling by airplane is far safer than driving (and that’s extremely hard to understate). In most years zero people die in commercial plane crashes in the US whereas tens of thousands die in car crashes per year in the US (~ about 40k). I would much rather fly on either Boeing or Airbus cross-country than drive from a safety perspective (it’s not even close and I wouldn’t think twice about flying Boeing tomorrow vs. driving). That said, I am curious about which airplane maker I should prefer from a safety perspective.

To compare Boeing and Airbus’s records, first I’ll load some helpful libraries,

library(tidyverse)
library(mdbr)

Next, I read in NTSB event data that can be found at https://data.ntsb.gov/avdata.

read_mdb("boeing-analysis/avall.mdb", "events") -> events
read_mdb("boeing-analysis/avall.mdb", "aircraft") -> aircraft

After reading in the NTSB data, I organized and prepare the data for analysis,

events %>%
  mutate(date = as.POSIXct(ev_date, format = "%m/%d/%y %H:%M:%S", tz = "UTC")) %>%
  left_join(aircraft, by = "ev_id") %>%
  distinct(ev_id, Aircraft_Key, .keep_all = T) -> d

# Count events by make and quarter
d %>%
  count(acft_make,
        accident_date = lubridate::floor_date(date, "half")) %>%
  # Fill in quarters with 0 to prevent common mistakes that can afflict analysis
  group_by(acft_make) %>%
  complete(accident_date = seq.POSIXt(min(accident_date), max(accident_date), by = "6 month"), 
           fill = list(n = 0)) %>%
  mutate(n_minus_avg = n - mean(n)) %>%
  ungroup() -> events_by_make

Boeing flies more flights than Airbus in the US. It’s important to take that into account, because we’d typically expect more events from a more popular maker. To do that I downloaded flight departure data from the Department of Transportation.

# Let's adjust for the number of departures performed
# https://www.transtats.bts.gov/databases.asp?Z1qr_VQ=E&Z1qr_Qr5p=N8vn6v10&f7owrp6_VQF=D
list.files("boeing-analysis/", pattern = ".csv") %>%
  Filter(function(x) { grepl("SEGMENT", x) }, .) %>%
  map_df(~ read_csv(paste0("boeing-analysis/", .x)) %>% mutate(file = .x)) %>%
  mutate(year = substr(file, 1, 4)) %>%
  janitor::clean_names() %>%
  select(year, month, aircraft_type, passengers, departures_performed, seats) %>%
  mutate(date = as.POSIXct(paste(year, sprintf("%02d", month), "01", sep = "-"),
                           format = "%Y-%m-%d",
                           tz = "UTC")) %>%
  group_by(date = lubridate::floor_date(date, "quarter"),
           aircraft_type) %>%
  left_join(
    read_csv("boeing-analysis/L_AIRCRAFT_TYPE.csv",
             show_col_types = FALSE) %>%
      janitor::clean_names() %>%
      rename(aircraft_type = code),
    by = "aircraft_type") %>%
  mutate(type = case_when(grepl("Boeing", description, ignore.case = T) ~ "Boeing",
                          grepl("Airbus", description, ignore.case = T) ~ "Airbus",
                          TRUE ~ "All other makers")) %>%
  group_by(date, type) %>%
  summarise(departures_performed = sum(departures_performed),
            passengers_flown = sum(passengers),
            seats_flown = sum(seats),
            .groups = "drop") %>%
  arrange(type, date) %>%
  ungroup() -> flights_per_quarter


events_by_make %>%
  mutate(type = case_when(grepl("Boeing", acft_make, ignore.case = T) ~ "Boeing",
                          grepl("Airbus", acft_make, ignore.case = T) ~ "Airbus",
                          TRUE ~ "All other makers")) %>%
  filter(type != "All other makers") %>%
  select(type, date = accident_date, n) %>%
  group_by(type, date) %>%
  summarise(events = sum(n), .groups = "drop") %>%
  inner_join(flights_per_quarter) %>%
  filter(date < max(date)) %>%
  mutate(events_per_100k_departures = events / (departures_performed / 1e5)) -> events_by_make2

Whew, now I have a nice data set ready for analysis,

events_by_make2 %>% 
  head(10)
## # A tibble: 10 × 7
##    type   date                events departures_performed passengers_flown
##    <chr>  <dttm>               <int>                <dbl>            <dbl>
##  1 Airbus 2008-01-01 00:00:00      8               262377         25696782
##  2 Airbus 2008-07-01 00:00:00      5               261690         27370578
##  3 Airbus 2009-01-01 00:00:00      7               243133         23373924
##  4 Airbus 2009-07-01 00:00:00      7               259044         27226711
##  5 Airbus 2010-01-01 00:00:00     14               235929         23329031
##  6 Airbus 2010-07-01 00:00:00      6               270520         29022592
##  7 Airbus 2011-01-01 00:00:00      9               251748         25399161
##  8 Airbus 2011-07-01 00:00:00      5               270947         30083653
##  9 Airbus 2012-01-01 00:00:00      7               260381         27634873
## 10 Airbus 2012-07-01 00:00:00      9               279822         31708432
## # ℹ 2 more variables: seats_flown <dbl>, events_per_100k_departures <dbl>

Let’s take a look at the number of NTSB events per 100k departures over time.

events_by_make2 %>%
  ggplot(aes(date, events_per_100k_departures, color = factor(type))) +
  geom_line(linewidth = 1) +
  geom_point(size = 3) +
  geom_hline(yintercept = 0) +
  ggthemes::scale_color_colorblind(name = "",
                                   guide = guide_legend(override.aes = list(linewidth = 5))) +
  theme_bw(20) +
  scale_x_datetime(date_breaks = "1 year", date_labels = "%Y") +
  theme(legend.position = "top",
        axis.text.x = element_text(
          color = "black",
          angle = 45, vjust = 1, hjust = 1),
        panel.grid = element_blank()) +
  ylab("NTSB events per 100k depatures") +
  ggtitle("NTSB events per 100k depatures") +
  scale_y_continuous(breaks = seq(0, 10, 2)) +
  xlab("Year")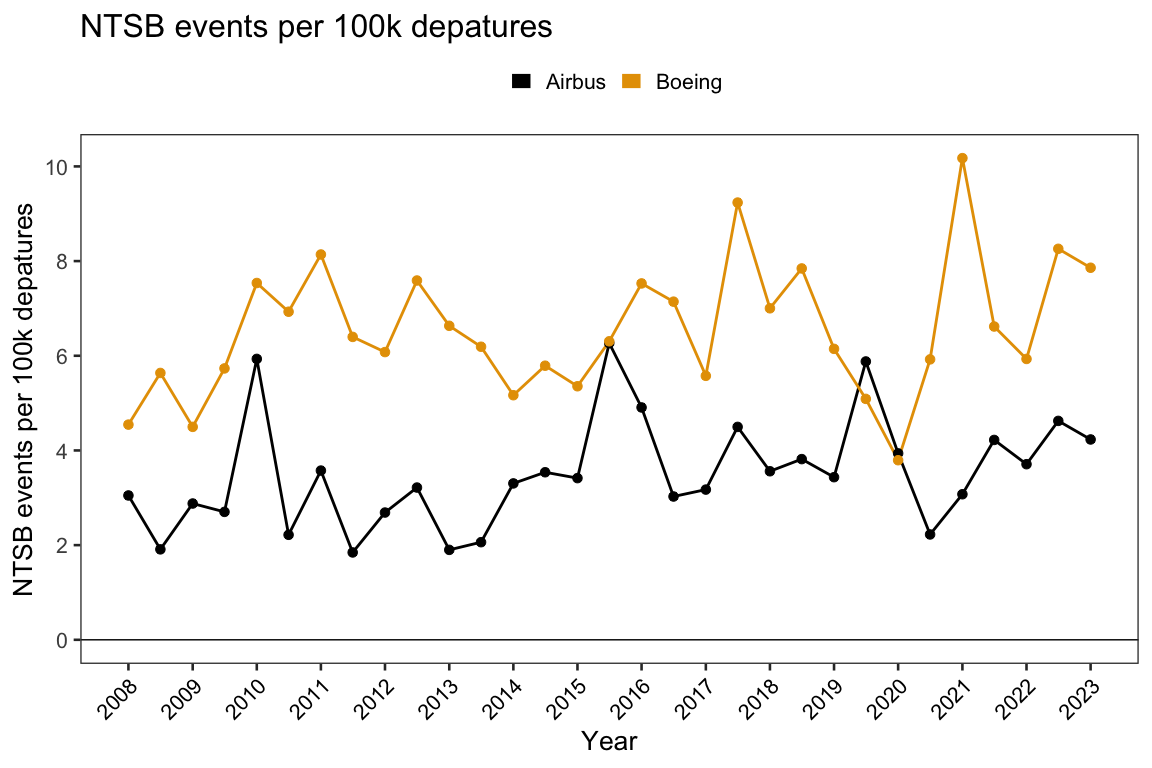

The result indicates to me that Boeing has more NTSB events per departure, about 6.5 per 100k departures vs. 3.8 per 100k for Airbus (assuming I haven’t made any errors). That’s about 1.7x more events per departure than Airbus! It’s important to note that I haven’t deeply looked into exactly what these events constitute, but clearly the NTSB felt they were worthy of recording.

That Airbus has fewer incidents than Boeing isn’t that surprising to me given the news. Also, I notice that Boeing’s advertisement for “reliability engineers” doesn’t require that those engineers have a degree in statistics. In my mind, if you’re hiring people who’s responsibility it is to perform statistical analysis in important situations, it’s best to hire statisticians with degrees in statistics. That seems obvious to me. Is this a Dunning-Kruger issue, or just reasonable economization? I’m not sure (Boeing’s stock value has significantly under-performed Airbus from 2019 to March 2024, a 49% decline vs. 42% growth, respectively).

Given the situation, it’s difficult to for me to understand why Boeing wouldn’t be advertising for reliability statisticians (as of March 16, 2024) at a minimum to regain public confidence, and I hope that’s something they quickly change. They owe it to their customers and shareholders.

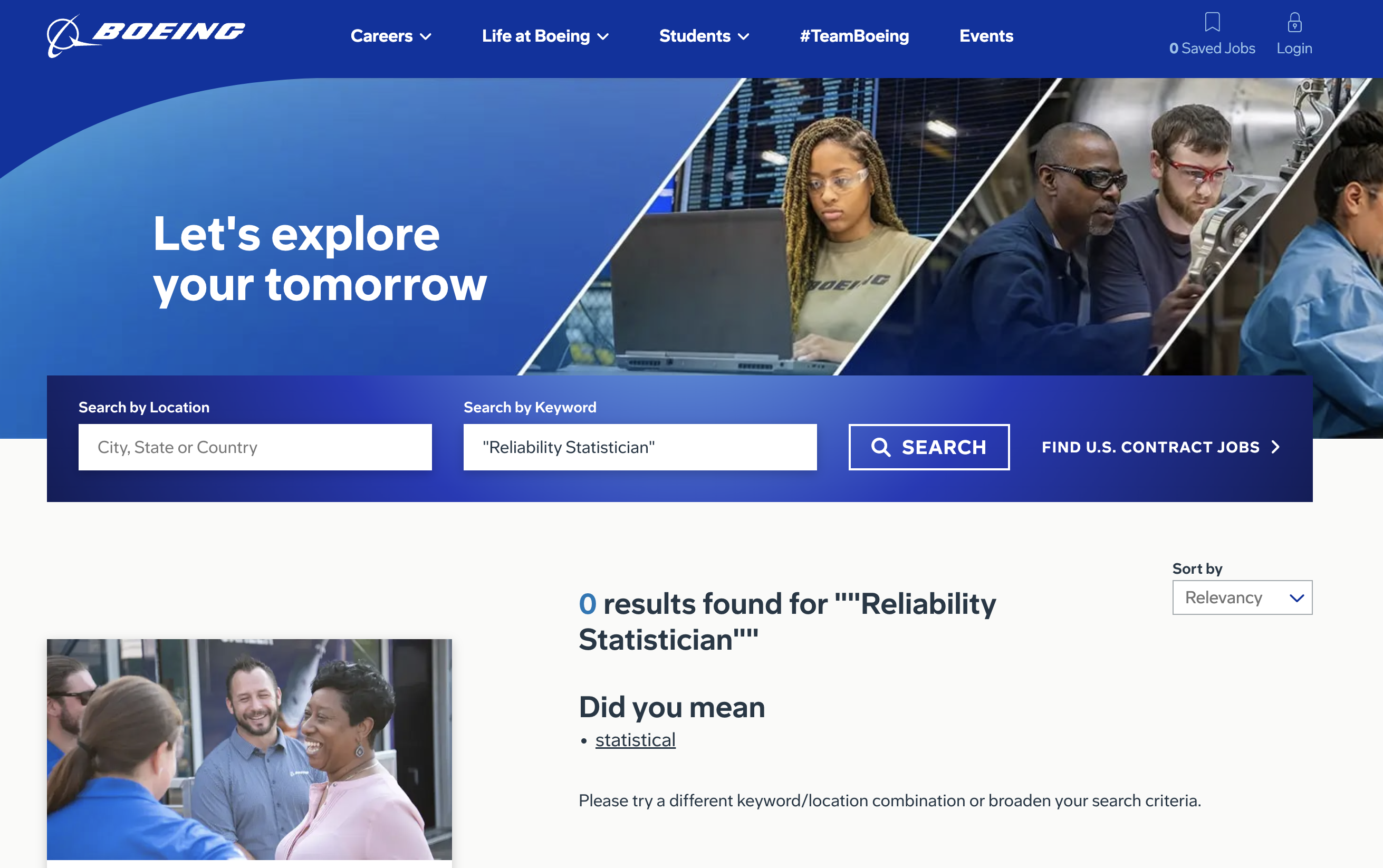
That said, this is clearly a long-term issue not a recent one. To address Joe’s original question: standing back, I’d say this falls more into the shark attack / confirmation bias camp (as opposed to representing a significant near-term uptick). Still, it is concerning that if my calculations are correct, Boeing has persistently more events per departure than Airbus. When it comes to the reliability of machines with the potential to harm many people, it’s important to pay attention to precursors to harm. From that point of view, I hope they’ll invest to close the apparent gap (like I mentioned).

That said, I still wouldn’t be concerned about flying in a plane produced by either company (and I don’t think you should let it bother you much either). I believe this is more of a money issue for Boeing than a safety issue. It’s hard to judge rare events using intuition– our brains just aren’t wired to accurately assess the risk of infrequent occurrences. Statistically speaking, air travel remains one of the safest modes of transportation available. The rigorous testing, maintenance, and oversight that aircraft from reputable manufacturers undergo are unparalleled. Both pilot training and aircraft engineering are constantly evolving to enhance safety and reduce the already low risk of accidents. It’s natural to feel apprehensive about flying, especially in light of high-profile incidents. However, it’s important to remember that millions of flights take off and land safely every year, a testament to the industry’s commitment to safety. So, while it’s wise to be aware of the risks, letting fear of flying limit your opportunities or dictate your travel choices is to ignore the overwhelming evidence of its safety.

# Assume 0 events given 0 departures by not including an intercept
lm(events ~ I(departures_performed / 1e5) : type - 1,
   data = events_by_make2) -> fit

summary(fit)
## 
## Call:
## lm(formula = events ~ I(departures_performed/1e+05):type - 1, 
##     data = events_by_make2)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -20.062  -4.151  -1.323   3.405  20.942 
## 
## Coefficients:
##                                          Estimate Std. Error t value Pr(>|t|)
## I(departures_performed/1e+05):typeAirbus   3.7716     0.3889   9.698 6.73e-14
## I(departures_performed/1e+05):typeBoeing   6.5120     0.1862  34.968  < 2e-16
##                                             
## I(departures_performed/1e+05):typeAirbus ***
## I(departures_performed/1e+05):typeBoeing ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 7.325 on 60 degrees of freedom
## Multiple R-squared:  0.9564, Adjusted R-squared:  0.955 
## F-statistic: 658.4 on 2 and 60 DF,  p-value: < 2.2e-16

@statwonk