Simulating right-censored weibull distributed data
suppressPackageStartupMessages({
library(dplyr)
library(purrr)
library(survival)
library(ggplot2)
library(glue)
library(ggthemes)
})
set.seed(0)Time-to-event data are extremely common in industry. Commonly one has timestamps from a log file and wants to gain some understanding of a conversion rate. We can borrow from the manufacturing industry and deploy a common technique called weibull analysis. Weibull analysis can get us a quick measurement of a really special statistic called the “characteristic life.” The characteristic life is the 0.632 quantile (aka 63.2 percentile) of a conversion rate under the weibull model.
What’s neat about the characteristic life is that its estimation over many different conversion rates can yield a way to compare a basket of conversion rate scales.
There’s a hitch though. These data are right-censored (Type 1 censored). We collect data from the start of some process and often we observe conversion but sometimes we do not. The remaining unconverted units could all convert the moment after we pull the data, or they might never convert. Thinking about how that would change the analysis can illustrate the damaging effects of naively including or excluding these units.
So we want to explore some Weibull data. Those that work with servers are often on the minute scales, however often one has a low conversion rate below 10 percent.
This scenario implies a long characteristic life, like say 500,000 minutes or about 350 days to reach 63.2% converted.
Also our shape parameter will definitely need to be less than 1 in this case. It’s well known that web and online conversion rates pack a fast and strong effect until the user flys away to another tab.
N <- 1e3 # observations to generate
shape <- 0.3 # lets give this distribution a shape that reflects a quick stimulus
# 500k minutes, if this is large, that must mean we have a low conversion rate in the first say hour
quantile_632 <- 5e5
(x <- rweibull(N, shape = shape, scale = quantile_632)) %>%
tibble(x = .) %>%
ggplot(aes(x = x)) + geom_histogram(colour = "black") +
ggtitle(glue("Histogram of random X ~ weibull(k = { shape }, lambda={ quantile_632 })")) +
xlab("Minutes")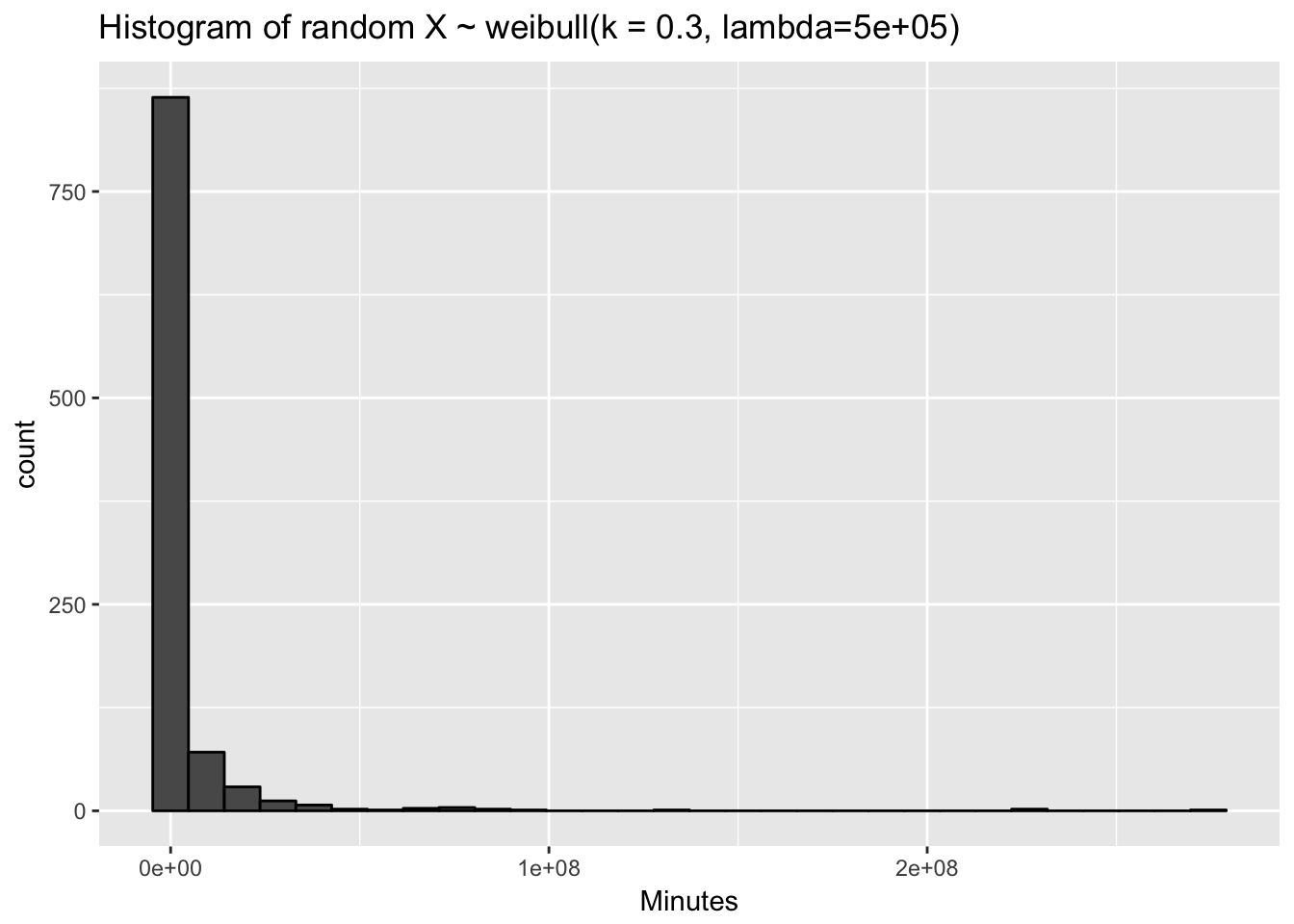
x %>% head()## [1] 309.6589 1281050.0947 481135.2745 71145.3971 204.5447
## [6] 2400666.2642There’s no built in R function for generating censored Weibull data. We can do that here. We generate two weibull series. Both share the same shape and scale parameters. This reflects that whether a unit is censored or not is independent from the time of death. Given a death time, I can’t tell you which of the internal mechnisms generated the data. In practice this assumption should be questioned.
rweibull_cens <- function(n, shape, scale) {
a_random_death_time <- rweibull(n, shape = shape, scale = scale)
a_random_censor_time <- rweibull(n, shape = shape, scale = scale)
observed_time <- pmin(a_random_censor_time, a_random_death_time)
censor <- observed_time == a_random_death_time
tibble(time = observed_time, censor = censor)
}It’s always prudent to check a random number generator by feeding it known parameters and then estimating those parameters.
rweibull_cens(1e6, 0.3, 5e5) %>%
flexsurv::flexsurvreg(Surv(time, censor) ~ 1, data = ., dist = "weibull")## Call:
## flexsurv::flexsurvreg(formula = Surv(time, censor) ~ 1, data = .,
## dist = "weibull")
##
## Estimates:
## est L95% U95% se
## shape 3.00e-01 2.99e-01 3.01e-01 3.31e-04
## scale 4.99e+05 4.94e+05 5.03e+05 2.40e+03
##
## N = 1000000, Events: 500928, Censored: 499072
## Total time at risk: 459042853980
## Log-likelihood = -6193941, df = 2
## AIC = 12387886For fun I’ll make sure that our confidence intervals mostly contain our known parameters. Here I’m generating 100 samples, then I change their color if they don’t include the “true” or “known” parameter.
seq_len(100) %>%
map(function(x) { rweibull_cens(N, shape = shape, scale = quantile_632) }) %>%
map(function(x) {
x$sample <- uuid::UUIDgenerate()
return(x)
}) %>%
map(function(x) {
survival::survreg(survival::Surv(time, censor) ~ 1, data = x, dist = "weibull",
control = survival::survreg.control(maxiter = 100)) %>%
broom::tidy() %>%
mutate(sample = unique(x$sample))
}) %>%
bind_rows() %>%
filter(term == "(Intercept)") %>%
mutate(lower = exp(conf.low), upper = exp(conf.high)) %>%
mutate(actual = quantile_632) %>%
mutate(miss = ifelse(actual < lower | upper < actual,
"Failed to include real parameter", "Included parameter")) %>%
ggplot(aes(y = factor(sample))) +
geom_errorbarh(aes(xmin = lower, xmax = upper, colour = factor(miss)), height = 0) +
geom_vline(aes(xintercept = unique(actual)), col = "red") +
ylab("Sample confidence interval") +
xlab("Confidence interval (horizontal lines) vs actual (vertical lines)") +
scale_color_discrete(name = "", guide = guide_legend(override.aes = list(size = 5))) +
theme_bw(18) +
theme(axis.text.y = element_blank(),
legend.position = "top",
panel.grid.major = element_blank(), panel.grid.minor = element_blank())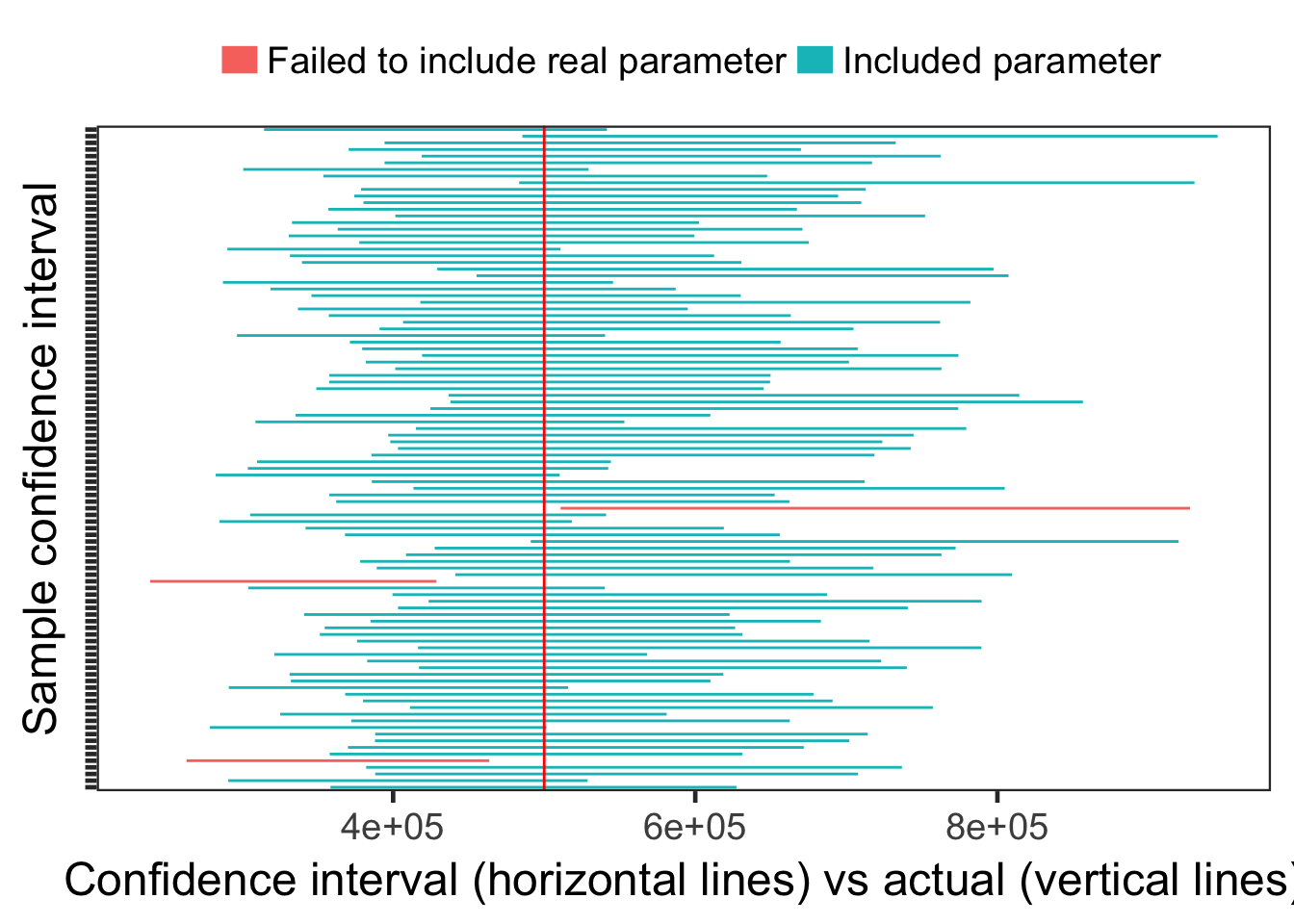
In the next plot, again I’ll signify the “true” value as a red line. I’ll show the distribution of estimates of that true value in repeated samples. I’d say the distribution captures the true value very well. Next I’ll take a visual look at the upper confidence interval bounds in repeated samples. Notice that sometimes the upper part of the confidence interval is below the true value.
seq_len(1e3) %>%
map(function(x) { rweibull_cens(N, shape = shape, scale = quantile_632) }) %>%
map(function(x) {
x$sample <- uuid::UUIDgenerate()
return(x)
}) %>%
map(function(x) {
survival::survreg(survival::Surv(time, censor) ~ 1, data = x, dist = "weibull",
control = survival::survreg.control(maxiter = 100)) %>%
broom::tidy() %>%
mutate(sample = unique(x$sample))
}) %>%
bind_rows() %>%
filter(term == "(Intercept)") %>%
mutate(lower = exp(conf.low), upper = exp(conf.high)) %>%
mutate(actual = quantile_632) %>%
select(estimate, upper) %>%
ggplot(aes(x = exp(estimate))) +
geom_histogram(colour = "black") +
geom_vline(xintercept = quantile_632, col = "red") +
geom_vline(aes(xintercept = upper), col = "blue", alpha = 0.2) +
xlab("Characteristic life (percentile 63.2%) aka 'lambda' or sometimes 'eta'") +
ggtitle("Weibull shape parameter")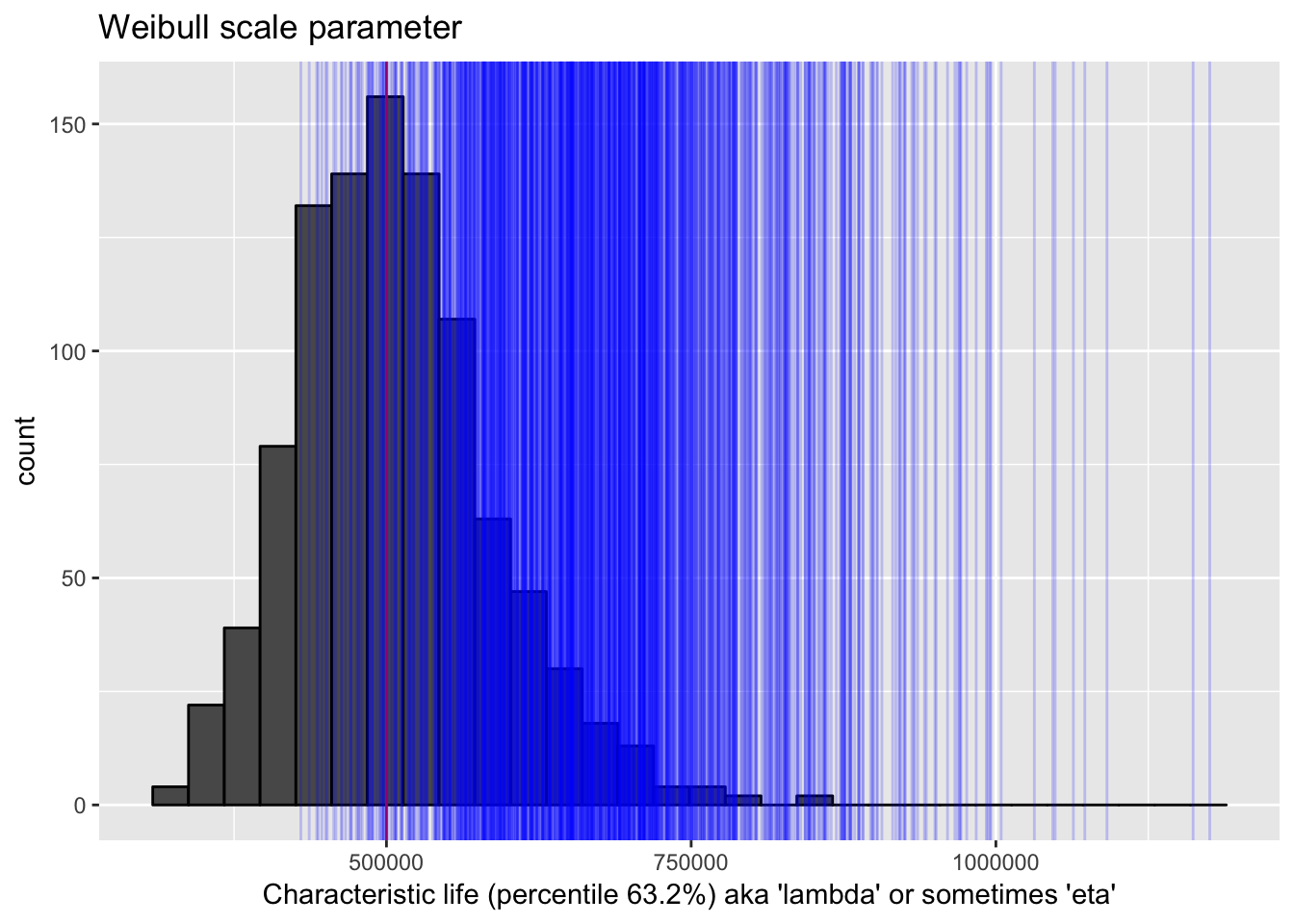
Now I’ll finish up by showing visually that indeed the 63.2% percentile is the 500k-th minute “characteristic life” that we originally chose as part of our random number generation.
seq_len(20) %>%
map(function(i) { rweibull_cens(N, shape = shape, scale = quantile_632) %>% mutate(group = i) }) %>%
bind_rows() %>%
mutate(group = factor(group)) %>%
survfit(Surv(time, censor) ~ group, data = .) %>%
plot(
fun = "event", xlim = c(0, 6e5), ylim = c(0, 0.7),
main = glue::glue(
"Conversion rate,\nn = 20, X ~ weibull(k = { shape }, lambda={ quantile_632 })"),
xlab = "Minutes", ylab = "Conversion rate")
abline(h = 0.632, col = "red", lwd = 2)
abline(v = 5e5, col = "red", lwd = 2)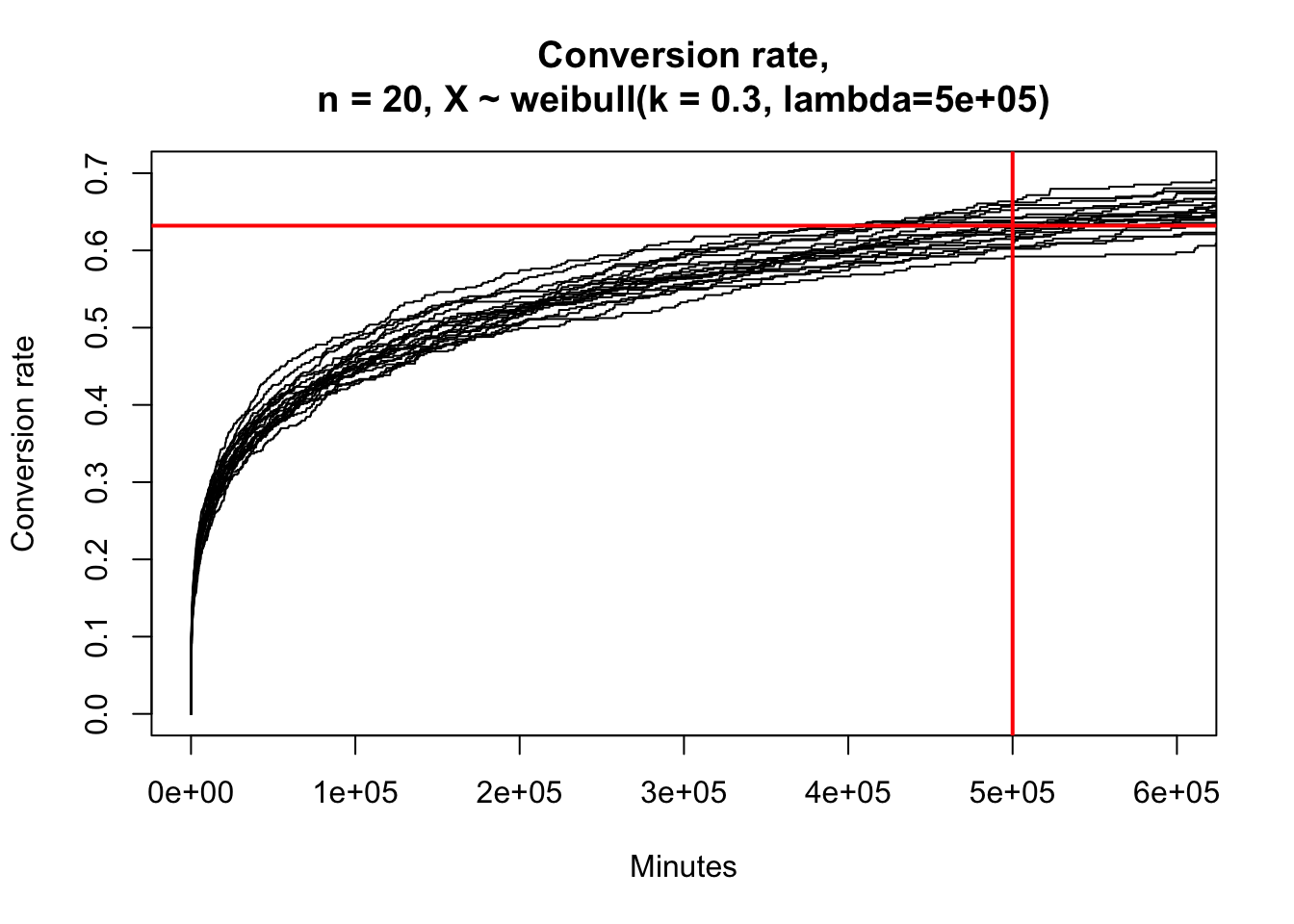
Thank you for jamming along!