Zero-inflated count data are pretty much everywhere. In fact there are typically many more processes going on in a given count dataset than zero-inflation. Zero-inflation itself may be the realization of serveral processes. These are but one set of random numbers generated from a homogenous zero-inflated negative binomial spec. Whether it’s worth the effort to tease out finer mixtures is a use-case dependent decision. Happy generating!

set.seed(1)
# install.packages('pscl')
suppressPackageStartupMessages({ library(tidyverse); library(reshape2); library(pscl) })
rzinb <- function(n, size, mu, proportion_zero) {
  fake_data <- rep(NA_real_, n)
  fake_data[which(rbinom(n, 1, prob = proportion_zero) == 0)] <- 0 # set the 0s
  nb_fake_data <- rnbinom(n, size = size, mu = mu) # generate a full set of nbs
  
  # fill in spaces left by 0s mask
  fake_data[is.na(fake_data)] <- nb_fake_data[is.na(fake_data)] 
  
  return(fake_data)
}
seq_len(300) %>%
  map(function(i) {
    N <- 400
    X <- rnorm(N) 
    x <- rzinb(n = N, 
               size = 1, 
               mu = exp(1 + X * 0.5), 
               proportion_zero = 0.5) %>%
      tibble(y = .) %>%
      mutate(x = X) %>%
      pscl::zeroinfl(y ~ x | 1, data = ., dist = "negbin")
    output <- x %>% coefficients() %>% as.list()
    output$theta <- x$theta
    return(output)
  }) %>%
  map(function(x) { as_tibble(x) }) %>%
  bind_rows() %>%
  mutate(proportion_zero = plogis(`zero_(Intercept)`)) %>%
  select(count_intercept = `count_(Intercept)`, slope = count_x, size = theta, proportion_zero) %>%
  reshape2::melt() %>%
  ggplot(aes(x = value)) +
  geom_density() +
  facet_wrap(~ variable, scales = "free")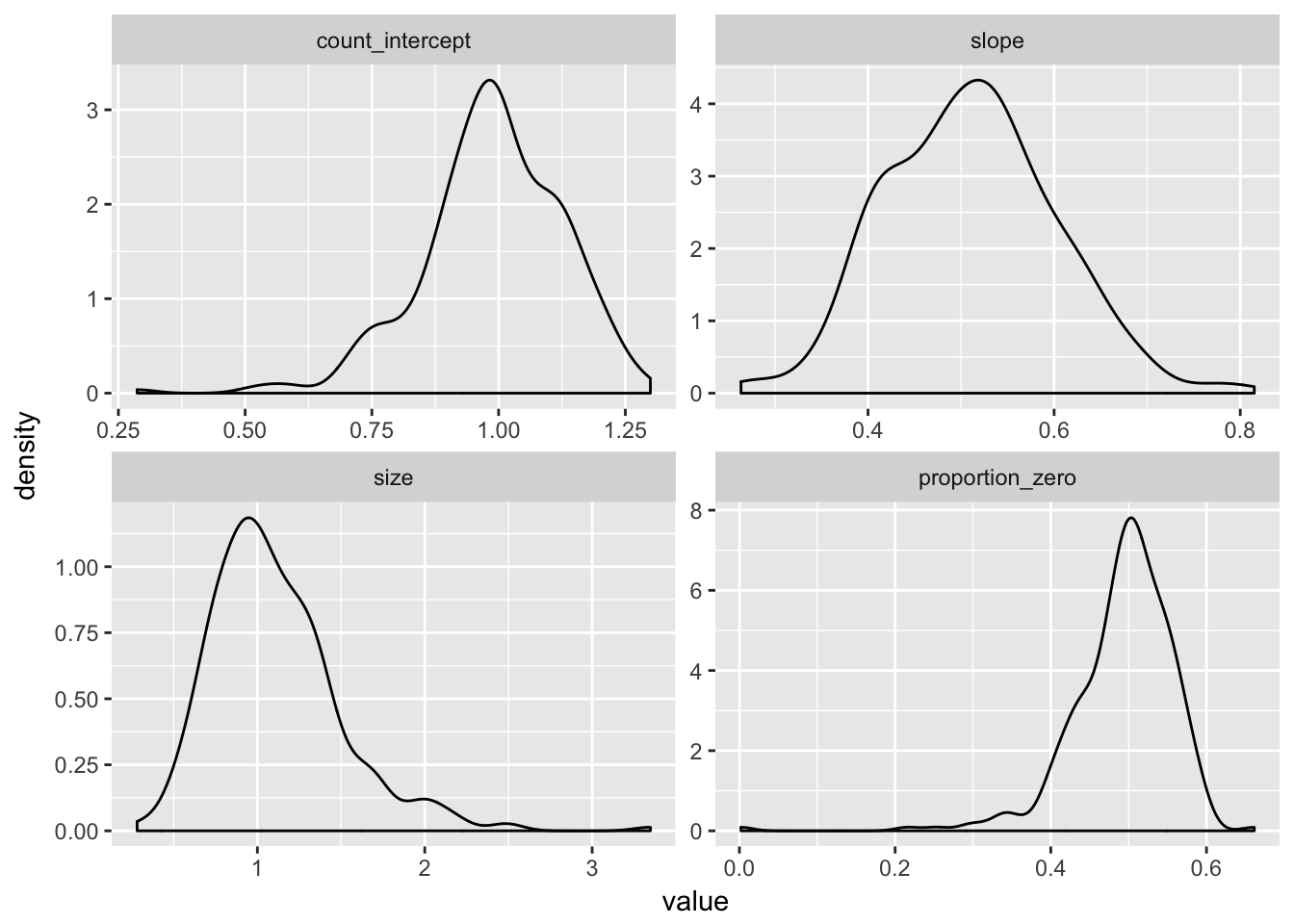

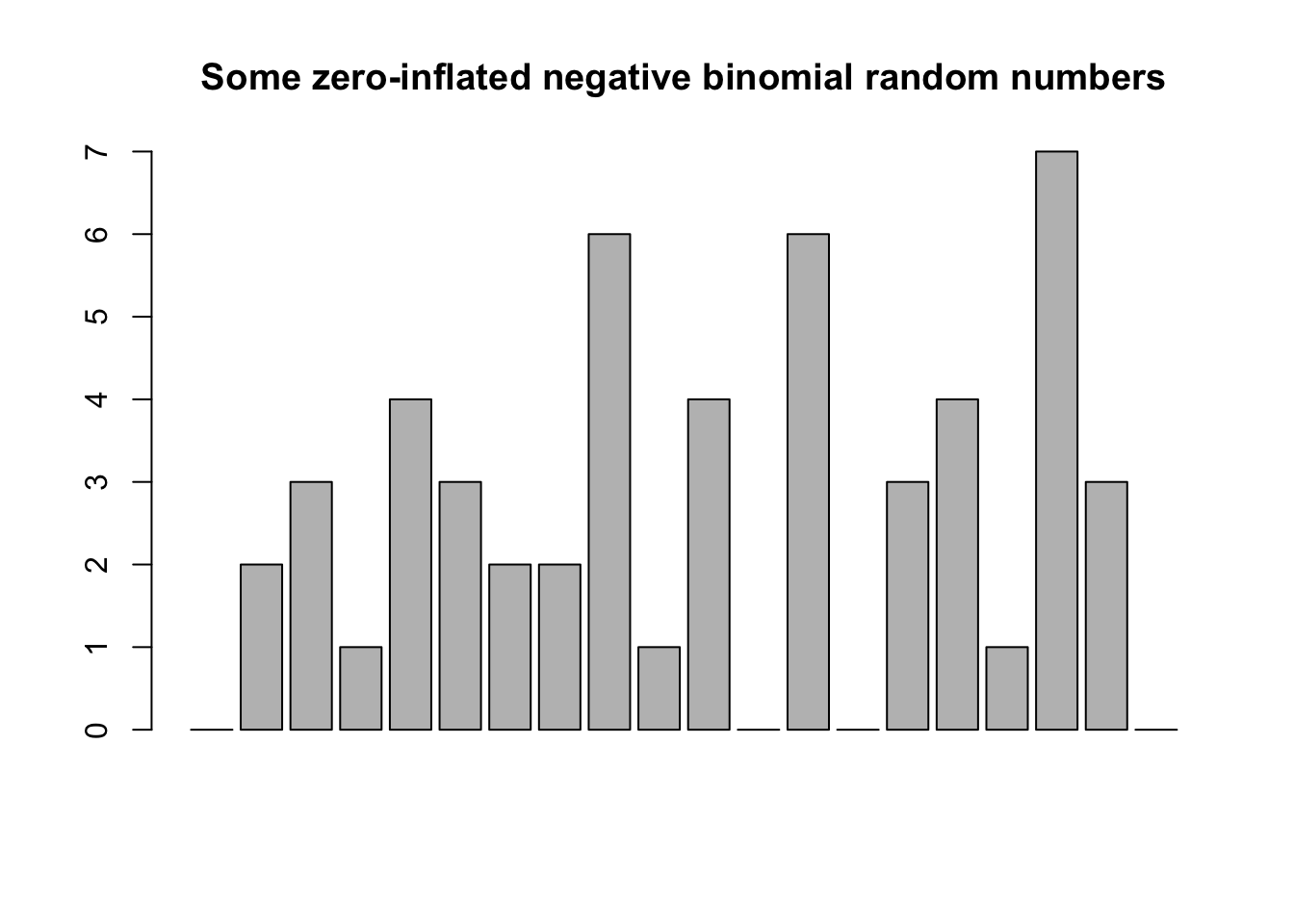
barplot(
  rzinb(20, size = 100, mu = 4, proportion_zero = 0.8), 
  main = "Some zero-inflated negative binomial random numbers")

@statwonk