Estimating right-censored weibull parameters
library(tidyverse)
library(survival)
library(brms)
library(tidybayes)
library(ggthemes)First I’ll repurpose a random right-censored weibull random number generator I wrote in a previous post. It took me a while to simplify and appreciate how to do this. The idea is that we’re drawing from two data generating processes. If the first (the censoring process) returns a randomnly generated time prior to that of a second generator, then the observation is censored otherwise we’ve observed death (conversion).
Therefore we have two data generating processes that are mixing together in these cases. If censoring is random, the death time process will shine through. Information in the censoring process will influence observed times.
rweibull_cens <- function(n, shape, scale) {
a_random_death_time <- rweibull(n, shape = shape, scale = scale)
a_random_censor_time <- rweibull(n, shape = shape, scale = scale)
observed_time <- pmin(a_random_censor_time, a_random_death_time)
censor <- observed_time == a_random_death_time
tibble(time = observed_time, censor = censor)
}
rweibull_cens(1e4, shape = 1, scale = 10) -> dFit using the common Frequentist approach,
d %>%
survival::survreg(Surv(time, censor) ~ 1, data = .) %>%
summary()##
## Call:
## survival::survreg(formula = Surv(time, censor) ~ 1, data = .)
## Value Std. Error z p
## (Intercept) 2.2916 0.0142 161.93 0.000
## Log(scale) -0.0169 0.0110 -1.54 0.124
##
## Scale= 0.983
##
## Weibull distribution
## Loglik(model)= -16561.6 Loglik(intercept only)= -16561.6
## Number of Newton-Raphson Iterations: 6
## n= 10000Fit using brms, a Bayesian model ready to have prior material incorporated.
d %>%
# Note cens uses the opposite 0/1 encoding of the survival package,
# I prefer the brms style personally. 0 for death, and 1 for censored.
mutate(censor = if_else(censor == 0, 1, 0)) %>%
brm(time | cens(censor) ~ 1, data = ., family = "weibull",
refresh = 2e3, cores = 4) -> bfit## Compiling the C++ model## Start samplingprint(bfit, digits = 3)## Family: weibull
## Links: mu = log; shape = identity
## Formula: time | cens(censor) ~ 1
## Data: . (Number of observations: 10000)
## Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
## total post-warmup samples = 4000
##
## Population-Level Effects:
## Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
## Intercept 2.285 0.015 2.255 2.316 1994 1.000
##
## Family Specific Parameters:
## Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
## shape 1.017 0.011 0.995 1.039 2183 1.000
##
## Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample
## is a crude measure of effective sample size, and Rhat is the potential
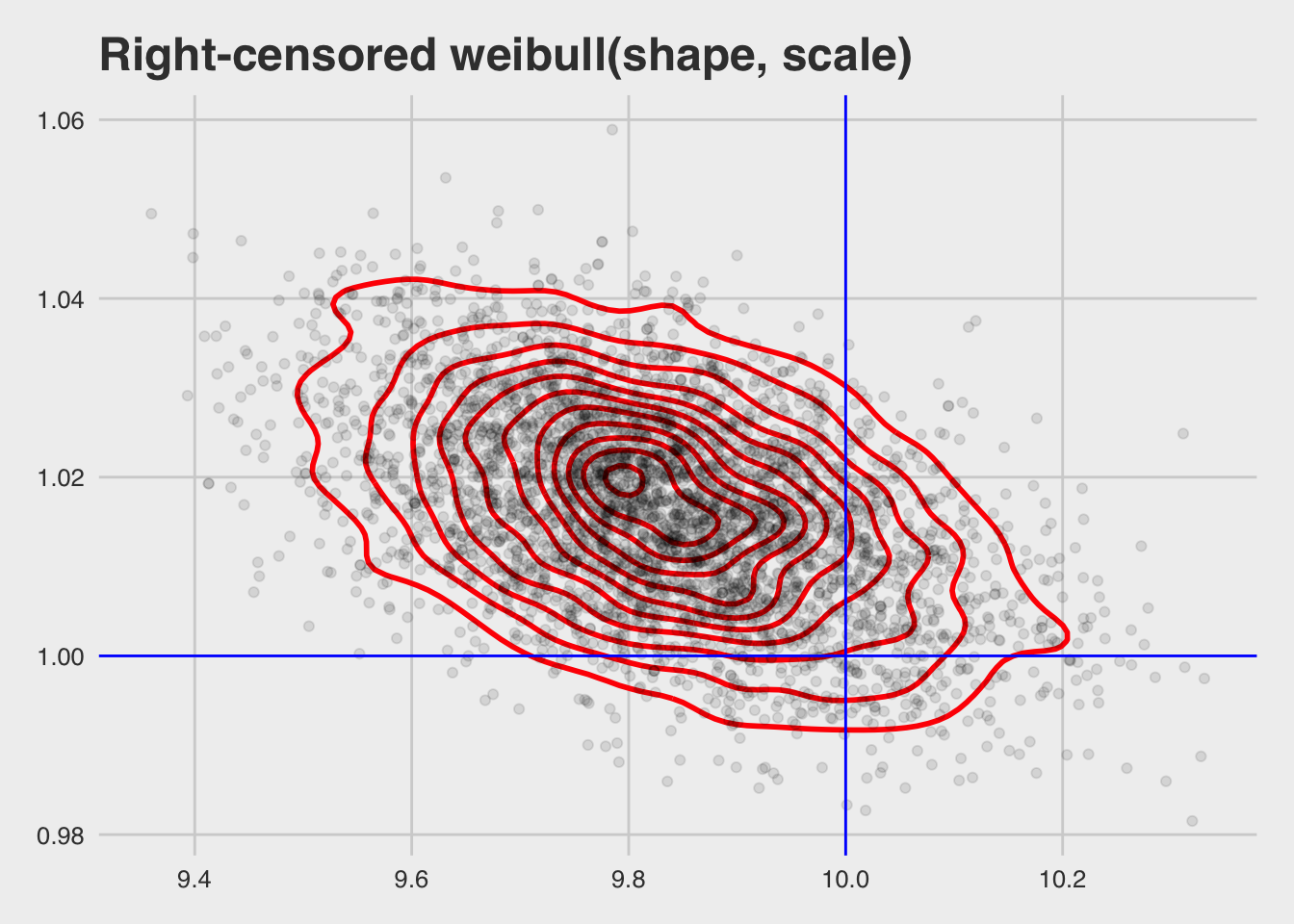
## scale reduction factor on split chains (at convergence, Rhat = 1).as_sample_tibble(bfit) %>%
mutate_at(vars(b_Intercept), exp) %>%
ggplot(aes(x = b_Intercept, y = shape)) +
geom_density_2d(colour = "red", size = 1) +
geom_point(alpha = 0.1) +
geom_hline(yintercept = 1, colour = "blue") +
geom_vline(xintercept = 10, colour = "blue") +
xlab("Scale") +
ylab("Shape") +
ggtitle("Right-censored weibull(shape, scale)") +
theme_fivethirtyeight()